When we talk about the shape of the earth we can refere it under two different concepts. The first one, concerns to the description of the geometric physic surface and the second one to the shape of the equipotencial real gravitical field, being this one, important to the characterization of its properties.
One of this equipotencial surfaces is particularly significative, namely the one that is coincident to the free surface of the oceans (discounting the meteorological effects) denominated of Geoid.
Geoid is an equipotencial surface of the earth gravitical field, being close to the average level of the ocean and extended hypothetically under the oceans. It is also designated of equipotencial surface of level zero (surface where the gravitical force has a same intensity in all it’s extension).
With the arriving of GPS (Global Position System/Navigation System with Time
And Ranging), the knowledge of the geoid as taken a crucial role in the vertical positioning, more specifically, becomes to exist the need to transform the ellipsoidal altitude obtained in GPS into an ortometric altitude. In this transformation, the knowledge of the geoid, acquires a crucial importance.
Having the geoid an irregular shape, and not being, therefore, passible of become mathematically represented, it’s easier then, to obtain the position of each physical surface of the earth relating to a mathematical figure. That figure is in practice an ellipsoid which get’s so close to the shape of the geoid, that it’s difference rarely exceeds 100 meters, Nevertheless, each country has to adopt has reference the most adequate ellipsoid to it’s region, since there are different values for the several elements of the ellipsoid regarding it’s spatial location.
The point where the surface of the ellipsoid touches the earth, it’s given the name of datum, which characterized starting from a surface of reference (horizontal datum) and a level surface (vertical datum – geoid).
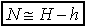
The geoid ondulation (N) is the distance between the geoidal surface and the ellipsoidal surface, counted along the plumb-line. This height is approximately equal to the difference between the ortometric (H) and ellipsoidal (h) altitude. The geoid ondulation differs on world from 107 to 85 meters, relating to ellipsoid of reference (WGS84). Therefore, can be written the following expression:
One of this equipotencial surfaces is particularly significative, namely the one that is coincident to the free surface of the oceans (discounting the meteorological effects) denominated of Geoid.
Geoid is an equipotencial surface of the earth gravitical field, being close to the average level of the ocean and extended hypothetically under the oceans. It is also designated of equipotencial surface of level zero (surface where the gravitical force has a same intensity in all it’s extension).
With the arriving of GPS (Global Position System/Navigation System with Time
And Ranging), the knowledge of the geoid as taken a crucial role in the vertical positioning, more specifically, becomes to exist the need to transform the ellipsoidal altitude obtained in GPS into an ortometric altitude. In this transformation, the knowledge of the geoid, acquires a crucial importance.
Having the geoid an irregular shape, and not being, therefore, passible of become mathematically represented, it’s easier then, to obtain the position of each physical surface of the earth relating to a mathematical figure. That figure is in practice an ellipsoid which get’s so close to the shape of the geoid, that it’s difference rarely exceeds 100 meters, Nevertheless, each country has to adopt has reference the most adequate ellipsoid to it’s region, since there are different values for the several elements of the ellipsoid regarding it’s spatial location.
The point where the surface of the ellipsoid touches the earth, it’s given the name of datum, which characterized starting from a surface of reference (horizontal datum) and a level surface (vertical datum – geoid).
The geoid ondulation (N) is the distance between the geoidal surface and the ellipsoidal surface, counted along the plumb-line. This height is approximately equal to the difference between the ortometric (H) and ellipsoidal (h) altitude. The geoid ondulation differs on world from 107 to 85 meters, relating to ellipsoid of reference (WGS84). Therefore, can be written the following expression:
Since the process of geometric levelling is quite expensive and takes lots of time and GPS has proved to be very useful in spatial positioning, there was the need to also obtain H using this system. Nevertheless, as the altitudes obtained with GPS (h) refers to the surface of the ellipsoid and not to the geoid, it is necessary to know N to get to H.
Dora Neto
Bibliography and full version of this article is presented in this blog with the name of "Geoid Ondulation".
No comments:
Post a Comment